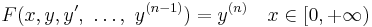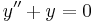Oscillation theory

In mathematics, in the field of ordinary differential equations, a non trivial solution to an ordinary differential equation

is called oscillating if it has an infinite number of roots, otherwise it is called non-oscillating. The differential equation is called oscillating if it has an oscillating solution. The number of roots carries also information on the spectrum of associated boundary value problems.

Examples

The differential equation

is oscillating as sin(x) is a solution.

Connection with spectral theory

Oscillation theory was initiated by Jacques Charles François Sturm in his investigations of Sturm–Liouville problems from 1836. There he showed that the n'th eigenfunction of a Sturm–Liouville problem has precisely n-1 roots. For the one-dimensional Schrödinger equation the question about oscillation/non-oscillation answers the question whether the eigenvalues accumulate at the bottom of the continuous spectrum.

Relative oscillation theory

In 1996 Gesztesy–Simon–Teschl showed that the number of roots of the Wronski determinant of two eigenfunctions of a Sturm–Liouville problem gives the number of eigenvalues between the corresponding eigenvalues. It was later on generalized by Krüger–Teschl to the case of two eigenfunctions of two different Sturm–Liouville problems. The investigation of the number of roots of the Wronski determinant of two solutions is known as relative oscillation theory.

See also

Classical results in oscillation theory are:

• Kneser theorem
• Sturm–Picone comparison theorem
• Sturm separation theorem

References

• Atkinson, F.V. (1964). Discrete and Continuous Boundary Problems, Academic Press.
• Gesztesy, F.; Simon, B.; Teschl, G. Zeros of the Wronskian and renormalized oscillation theory, Am. J. Math. 118, 571–594 (1996).
• Kreith, K. (1973). Oscillation Theory, Lecture Notes in Mathematics 324, Springer.
• Krüger, H; Teschl G. Relative oscillation theory, weighted zeros of the Wronskian, and the spectral shift function, Commun. Math. Phys. 287:2, 613–640 (2009).
• J.C.F. Sturm, Memoire sur les equations diferentielles lineaires du second ordre, J. Math. Pures Appl. 1 (1836), 106–186.
• Swanson, C.A. (1968). Comparison and Oscillation Theory of Linear Differential Equations, Academic Press.
• Teschl, Gerald (2011). Ordinary Differential Equations and Dynamical Systems. American Mathematical Society. http://www.mat.univie.ac.at/~gerald/ftp/book-ode/. 
• Weidmann, Joachim (1987). Spectral Theory of Ordinary Differential Operators, Lecture Notes in Mathematics 1258, Springer.